粘弹性动力力学分析导论“，

粘弹性是一种材料的性质，它表现出弹性或弹簧性质和粘性或流动性质的某种组合。

动力力学分析是通过对试验试样施加正弦变化的力并测量产生的应变响应来进行的。通过分析材料在一个周期内的响应，可以确定其弹性弹簧样存储模量和粘性或流动样损失模量(假想)。复模量是存储和损失(虚)模量的矢量和，用于表征粘弹性材料。由于可以计算每个循环的模量值，DMA是一种测量一定温度和频率范围内粘弹性材料行为的高效方法。

粘弹性与医学应用

像塑料一样，人体生物材料也表现出粘弹性。因此，动态力学分析可用于测量肌腱、组织、医疗器械等的粘弹性。此外，由于健康组织和病变组织的模量值不同，医生和科学家已经开始使用DMA作为检测癌症的诊断工具。对于绝大多数的医疗应用，DMA是在体外的工作台上进行的。然而，随着更复杂仪器的开发，DMA可能成为一种有效的诊断工具，可以在现场部署。

表征材料行为

不同类型的材料在不同的加载条件下，应力和应变之间的关系随时间而变化。如果应力和应变之间的关系是线性的和时间无关的，那么材料是弹性的，胡克定律描述了它的行为。

胡克定律:F = Kx

式中，F =施加力，K =弹簧常数，x =产生位移。

金属只要不超过其屈服点或暴露在高温下，就会表现出钩状行为。然而，大多数材料根据其加载条件表现出复杂的行为。正因为如此，他们的反应被解构为易于理解的理想化行为，以简化他们的分析。

弹性行为-大多数材料在施加小应力时表现出弹性或接近弹性。如图1所示，对于较小的应力s，可以得到立即的弹性应变响应e，只要应力保持固定，应变就保持固定，在去除力后立即降为零。大多数弹性材料是线性弹性的，因此，应力-应变行为成正比。

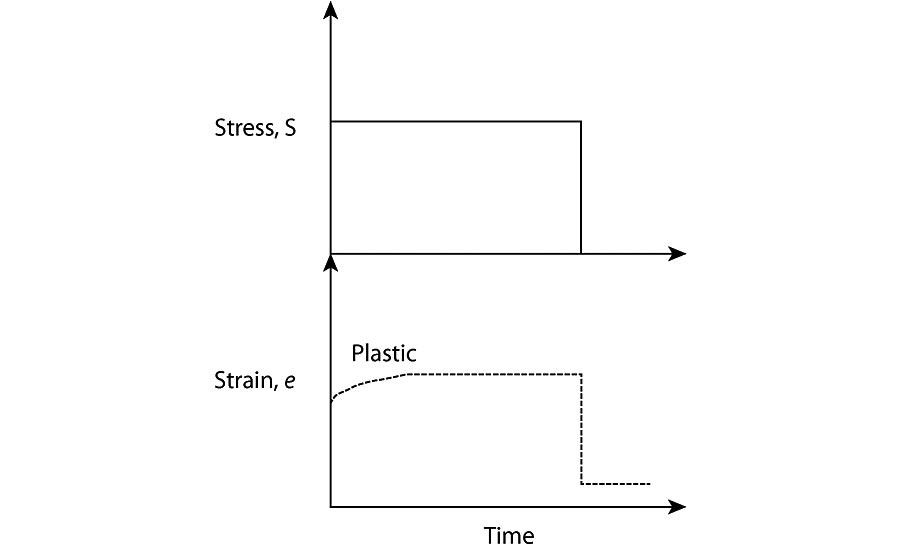
塑料的行为-如果应力超过弹性极限，那么应力和应变之间的关系不再成正比，可以成为时间依赖。在某些材料中，如图2所示，应力完全施加后，应变仍会持续增加一段时间。然而，去除应力后留下的应变是永久的，与时间无关的，被定义为塑性应变。

粘弹性行为-一些材料在快速加载后表现出弹性行为，然后以递减的速率缓慢而连续地增加应变。如图3所示，去除应力后，初始弹性恢复后，应变持续减小。

表现出粘弹性行为的材料受到施加应力或应变速率的显著影响。应力速率越慢，相应的应变越大。相反，应变速率越慢，对应的应力越低，如图4所示。

显示粘弹性行为的材料

生物制品、塑料、合成纤维和高温下的金属都是粘弹性材料的例子。粘弹性材料是时间相关的，这也使得它们应变率敏感。上图4分别是在应变速率为20%/min、200%/min和2000%/min时，聚丙烯带材在拉伸载荷下的应力-应变响应。图中显示应变速率越快，最大应力越大，断裂伸长率越低．对于那些比较批次之间相对强度的同类粘弹性材料，图4说明了在相同应变率下测试每个样品的重要性。

粘性材料，如水，抵抗剪切流动，并在施加应力时随时间线性应变。弹性材料在拉伸时发生应变，一旦应力消除，就立即恢复到原来的状态。粘弹性材料具有这两种特性的元素，因此，表现出随时间变化的应变。这意味着对应力输入的应变响应延迟，导致能量损失。

粘弹性行为通常发生在同一材料的不同时间尺度上。以恒定频率施加振荡应力或扫过频率范围的动态试验用于测量短时间内(通常在几秒内)的延迟应变响应。在高松弛时间(长达1小时)发生的响应通过实验来测量，其中材料要么保持恒定应变并随时间跟踪应力(应力松弛测试)，要么保持恒定应力并随时间跟踪应变(蠕变测试)。

动力力学分析

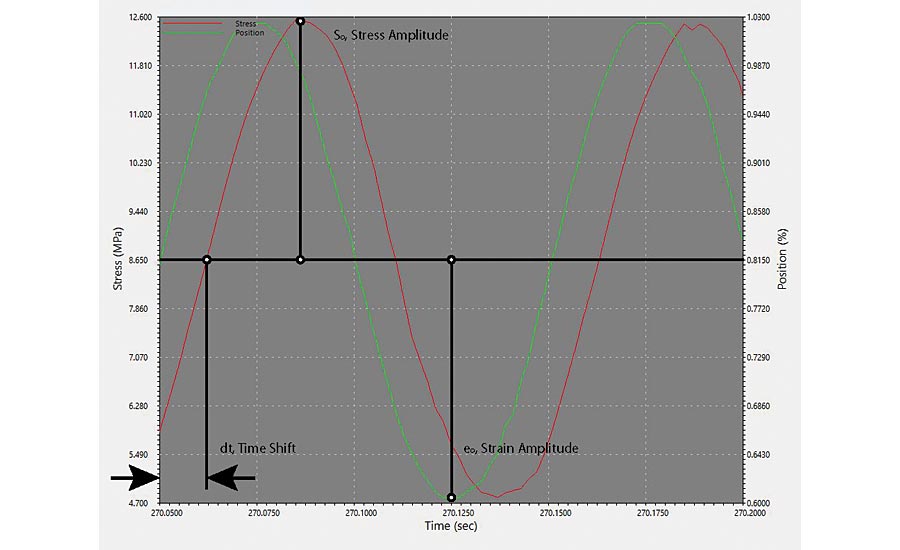
动态力学分析是通过对试样施加不同频率的振荡应力并分析所施加应力的应变响应来进行的。下面的图5描述了只加载拉伸的聚丙烯样品的正弦应力波形和响应应变波形。利用应变响应的时滞或相移来量化其粘性行为;应力应变响应的斜率与其弹性特性有关。这些特性通常被描述为热量损失能量的能力(阻尼)和从变形中恢复的能力(弹性)。

试样在正弦应力幅值控制波形下会发生正弦变形。如果材料保持在其线性粘弹性区域内，响应将是可重复的。在任何给定时间，施加的应力S(t)为:

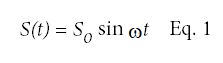
在哪里S (t)是当时的压力，t;年代_o为最大应力或应力幅值;ω是振荡频率。应变响应将取决于样品的粘性和弹性行为，并由式2控制，其中e (t)是时刻的弹性应变，t e_o为最大应变或应变振幅，θ为应力-时间波形和应变-时间波形之间的相移。

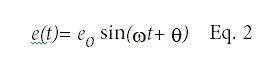
对于纯弹性或钩状材料，相移θ=0和

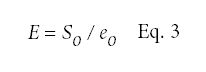
式中E =弹性模量。对于纯粘性材料，相移θ = ϖ /2，弹性模量未定义。式2表示弹性应变对正弦变化应力的响应。相等周期T的两个正弦波之间的相位角θ为:

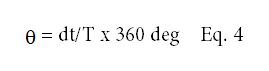
式中，dt=应力-时间波形与应变-时间波形之间的时移，T =振荡周期。

三角函数允许我们将Eq. 2重写为:

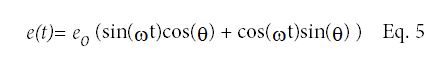
同相弹性应变为:

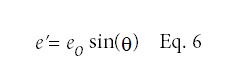
失相虚粘应变为:

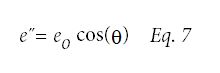
相内应变和相外应变的矢量和得到复应变e*。

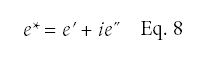
为了总结动态力学分析，试样受到振幅为S的正弦变化应力_o，频率f或周期T (1/f)，振幅e_o，测量得到的应变波形的时移dt。由此，相位滞后或损失角θ由式4计算，弹性模量或存储模量Eʹ由:

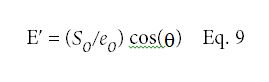
由于摩擦和内部运动而损失的能量量称为损失模量E，由以下公式表示:

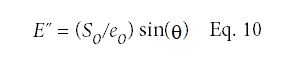
相位滞后或损失角的正切tan(θ)被称为损失正切或阻尼因子，并提供了由于材料的粘性性质而损失多少能量的测量。从图5中，我们可以确定聚丙烯样品的以下粘弹性特性。

Dt = 0.012秒

T = 0.1秒(10hz)

So = (12.521 - 4.779)/2 = 3.871 Mpa

e_o= (1.0244-0.6049)/(2 × 100) = 0.00209 mm/mm

根据公式4、9和10，计算损耗角、存储模量和损耗模量为:

Q = 0.012/0.1 x 360 = 43.2度

Eʹ= 3.871/0.00209 x cos (43.2) = 1,350 Mpa

E“= 3.871/0.00209 × sin(43.2) = 1268兆帕

此外，损耗tan, tan(θ) = tan(43.2) = 0.939。

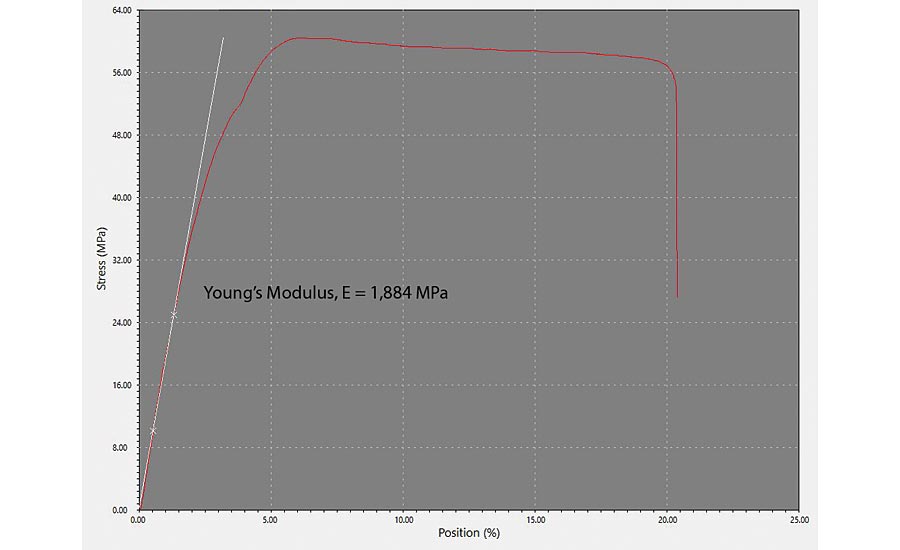
ASTM D638塑料拉伸性能的标准试验方法规定了聚丙烯杨氏模量的测定。图6为拉伸至破坏的聚丙烯试样的应力-应变图。

由图6可知，杨氏弹性模量为:

E = 1884 MPa

结论

简要介绍了动态力学分析和材料的粘弹性。DMA已被证明是一种简单而有效的方法，可以确定聚合物和塑料在一定温度和频率范围内的力学行为。新材料和诊断仪器的发展需要对粘弹性和如何测量其行为有更多的了解。ADMET动态测试系统对金属、塑料、纺织品、粘合剂、医疗设备和其他产品和部件进行疲劳测试。我们的系统和动态控制器精确计算峰值负载，伸长率，伸长模量，断裂屈服等。

点击下面的ADMET动态试验机或2020欧洲杯亚博 我们的销售工程师之一，详细讨论您的测试应用程序。

动态测试系统手册

本文由ADMET首席执行官理查德·格尼(Richard Gedney)撰写发表在《质量》杂志上2019年2月1日。